[edit]
1 개요 #
linear regression은 lm() 함수를 이용하면 된다. 이 문서의 목적은 최적화를 알아보기 위함이므로 optim() 함수를 이용하여 cost function()을 만들어 최적화하는 방법을 알아보겠다.
[edit]
2 data 준비 #
trees 데이터셋을 이용할 것인데, 컬럼명이 대문자라 코딩하기 귀찮으니 소문자로 변경하자.
df <- trees colnames(df) <- tolower(colnames(df)) head(df)
데이터가 준비되었다.
[edit]
3 simple regression #
독립 변수가 1개일 경우을 simple regression이라고 한다. lm()을 사용하면 간단히 할 수 있다.
lm.out <- lm(volume ~ girth, data=df) summary(lm.out)
결과
> summary(lm.out)
Call:
lm(formula = volume ~ girth, data = df)
Residuals:
Min 1Q Median 3Q Max
-8.065 -3.107 0.152 3.495 9.587
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -36.9435 3.3651 -10.98 7.62e-12 ***
girth 5.0659 0.2474 20.48 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.252 on 29 degrees of freedom
Multiple R-squared: 0.9353, Adjusted R-squared: 0.9331
F-statistic: 419.4 on 1 and 29 DF, p-value: < 2.2e-16
위 결과는 최소제곱법으로 최적화된 결과로 아래와 같은 회귀식을 만들 수 있다.
volume = 5.0659 * girth - 36.9435
5.0659은 가중치고, -36.9435는 바이어스다. 이것을 수동으로 해보자. 가설은 다음과 같다.
H(x) = wx + b
최적화할 함수 즉, cost function은cost(w,b) = avg((H(x) - y)^2)
cost.f <- function(par, x, y){
w <- par[1]
b <- par[2]
H <- w*x + b
mean((H - y)^2)
}
result <- optim(par = c(0, 0), cost.f, x = df$girth, y = df$volume)
result
결과
> result
$par
[1] 5.066008 -36.945325
$value
[1] 16.91299
$counts
function gradient
103 NA
$convergence
[1] 0
$message
NULL
위 결과를 보면
- w = 5.066008
- b = -36.945325
[edit]
4 multi regression #
독립 변수가 2개 이상인 경우를 multi regression이라고 한다. multi regression도 마찬가지로 lm() 함수를 이용하는 것과 cost function을 만들어 최적하는 방법을 써보자. 먼저 lm() 함수를 이용하면 다음과 같은 결과를 얻을 수 있다.
lm.out <- lm(volume ~ girth + height, data=df) summary(lm.out)
결과
> summary(lm.out)
Call:
lm(formula = volume ~ girth + height, data = df)
Residuals:
Min 1Q Median 3Q Max
-6.4065 -2.6493 -0.2876 2.2003 8.4847
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -57.9877 8.6382 -6.713 2.75e-07 ***
girth 4.7082 0.2643 17.816 < 2e-16 ***
height 0.3393 0.1302 2.607 0.0145 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.882 on 28 degrees of freedom
Multiple R-squared: 0.948, Adjusted R-squared: 0.9442
F-statistic: 255 on 2 and 28 DF, p-value: < 2.2e-16
이제 cost function을 만들어야하는데, 문제는 독립변수가 n개 생겨 다음과 같이 hypothesis가 복잡해졌다는 것이다.
H(x) = w1x1 + w2x2 + ... + b
이것을 단순화시키려면 대수적으로 접근해야하는데, 이것을 행렬로 취급하면 쉬워진다. 즉,
H(X) = WX + b
와 같이 대문자 W와 대문자 X를 행렬로 취급하여 H()를 만들면 simple regression과 같이 생각할 수 있게 된다. b도 행렬 X에 포함시켜 더욱 단순하게
H(X) = WX
와 같이 만들 수 있다. R로 cost function을 만들기 전에 우선 b를 데이터셋에 포함시키는데, 1로 세팅하면 된다. b <- 1 tmp <- cbind(b, df)
optim() 함수의 par 파라미터는 초기값을 주는 것인데 행렬의 곱(inner product)을 하려면 수학적 규칙을 맞춰야 한다. 예를 들면,
- M1 = 3행 2열
- M2 = 3행 2열
cost.f <- function(par, X, y){
W <- as.matrix(par)
X <- as.matrix(X)
mean((X%*%W - y)^2)
}
cost function을 작성했으니 이제 최적화 해보자.
result <- optim(par = c(0, 0, 0), cost.f, X = tmp[1:3], y = tmp[4]) result
결과
> result
$par
[1] -57.9996505 4.7082120 0.3394336
$value
[1] 13.61037
$counts
function gradient
238 NA
$convergence
[1] 0
$message
NULL
결과를 보면 lm() 함수와 거의 유사하다.
[edit]
5 응용 #
다음과 같이 이상치가 섞인 데이터가 있다.
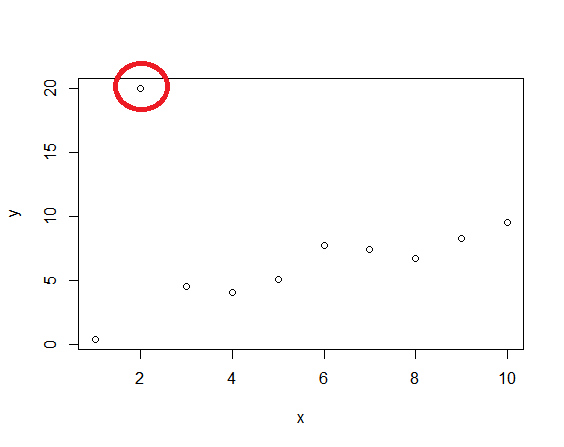
set.seed(123) mydata <- within(data.frame(x=1:10), y <- rnorm(x, mean=x)) mydata$y[2] <- 20 plot(mydata)--출처: http://www.alastairsanderson.com/R/tutorials/robust-regression-in-R/

lm() 함수는 최소제곱법으로 이상치에 취약하다. lm()함수를 쓰면 다음과 같은 결과를 얻는다.
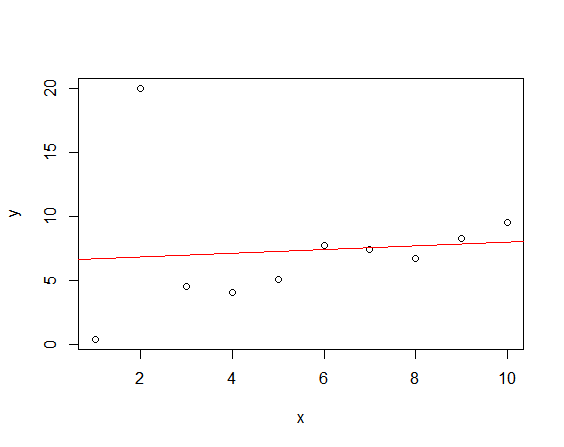
lm.out <- lm(y~x, data=mydata) plot(mydata) abline(lm.out, col="red")

최소제곱법 말고 다른 방법을 사용해보도록 하자. 실제값과 추정치의 차이에 제곱을하여 차이가 크면 패널티를 줬지만, 여기에서는 평균 절대 편차(MAD, mean absolute deviation)로 패널티를 주지 말아보자.
cost.f <- function(par, x, y){
w <- par[1]
b <- par[2]
H <- w*x + b
mean(abs(H - y))
}
result <- optim(par = c(0, 0), cost.f, x = mydata$x, y = mydata$y)
result
결과
> result
$par
[1] 0.8849192 0.7047651
$value
[1] 2.37167
$counts
function gradient
249 NA
$convergence
[1] 0
$message
NULL
그림으로 비교해보자.
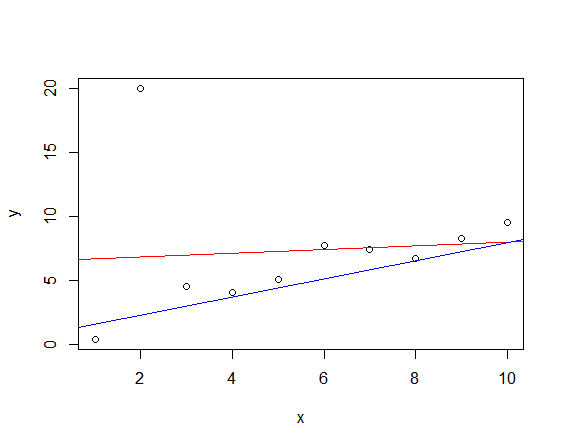
plot(mydata) abline(lm.out, col="red") abline(a = result$par[1], b = result$par[2], col = "blue")

뭔가 lm() 함수를 쓴 것보다 괜찮아 보이긴 한다. 하지만, 만족스럽지는 않다.
참고로 robust regression의 결과는 다음과 같다. black line이 rlm()의 결과다.
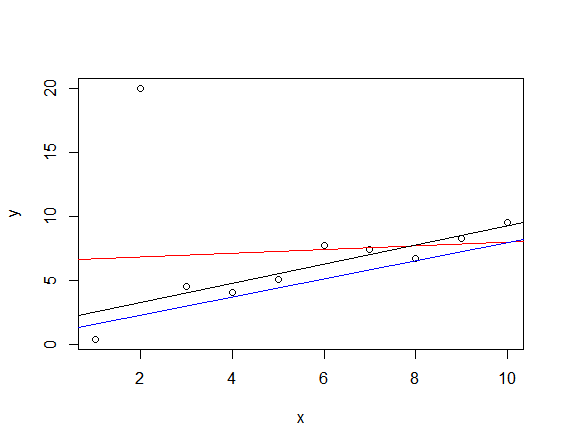
참고로 robust regression의 결과는 다음과 같다. black line이 rlm()의 결과다.
library(MASS) rlm.out <- rlm(y~x, data=mydata) abline(rlm.out)

음.. 좋다. 잘 fitting됬다.
![[-] [-]](/moniwiki/imgs/plugin/arrup.png)
![[+] [+]](/moniwiki/imgs/plugin/arrdown.png)