[edit]
1 лІ лҘҙлҲ„мқҙмқҳ мӢңн–ү #
- м„ұкіө лҳҗлҠ” мӢӨнҢЁ
- мӮ¬кі лҳҗлҠ” л¬ҙмӮ¬кі
- м–‘н’Ҳ лҳҗлҠ” л¶Ҳлҹүн’Ҳ
- лі‘м—җ к°җм—ј лҳҗлҠ” 비к°җм—ј
- лҸҷм „мқ„ лҚҳм ё м•һл©ҙ лӮҳмҳҙ лҳҗлҠ” л’·л©ҙ лӮҳмҳҙ
- м°¬м„ұ лҳҗлҠ” л°ҳлҢҖ
[edit]
2 лІ лҘҙлҲ„мқҙ мӢңн–үм—җ лҢҖн•ң к°Җм • #
- к°Ғ мӢңн–үмқҖ м„ұкіөкіј мӢӨнҢЁмқҳ л‘җ к°Җм§Җ мӮ¬кұҙл§Ңмқ„ к°Җ진лӢӨ.
- к°Ғ мӢңн–үм—җм„ң м„ұкіөн• нҷ•лҘ мқҖ p, мӢӨнҢЁн• нҷ•лҘ мқҖ q = 1 - pлҘј к°Җ진лӢӨ.
- к°Ғ мӢңн–үмқҖ м„ңлЎң лҸ…лҰҪмңјлЎң к°Ғ мӢңн–үмқҳ кІ°кіјк°Җ лӢӨлҘё мӢңн–үмқҳ кІ°кіјм—җ мҳҒн–Ҙмқ„ лҜём№ҳм§Җ м•ҠлҠ”лӢӨ.
[edit]
3 мқҙн•ӯ분нҸ¬мқҳ м •мқҳ #
нҷ•лҘ ліҖмҲҳ Xмқҳ 분нҸ¬к°Җ мқҙн•ӯ 분нҸ¬лҘј л”°лҘј кІҪмҡ° X ~ Binomial(n,p)лЎң н‘ңкё°н•ҳл©°, к·ё нҷ•лҘ м§Ҳлҹүн•ЁмҲҳ(PMF) мӢқмқҖ лӢӨмқҢкіј к°ҷлӢӨ.
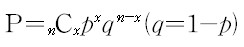
n: лІ лҘҙлҲ„мқҙ мӢңн–үмқҳ л°ҳліөнҡҹмҲҳ
p: к°Ғ мӢңн–үм—җм„ң м„ұкіөн• нҷ•лҘ (0 < p < 1)
x: nлІҲ мӢңн–үмӨ‘ м„ұкіөмқҳ нҡҹмҲҳ
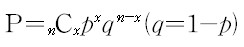
n: лІ лҘҙлҲ„мқҙ мӢңн–үмқҳ л°ҳліөнҡҹмҲҳ
p: к°Ғ мӢңн–үм—җм„ң м„ұкіөн• нҷ•лҘ (0 < p < 1)
x: nлІҲ мӢңн–үмӨ‘ м„ұкіөмқҳ нҡҹмҲҳ
[edit]
4 мқҙн•ӯ분нҸ¬мқҳ мҳҲ #
- лҸҷм „лҚҳм§Җкё°лҘј 10лІҲ мӢңн–үн• кІҪмҡ° м•һл©ҙмқҙ лӮҳмҳЁ нҡҹмҲҳ
- мӢ м•Ҫмқ„ ліөмҡ©н•ң нҷҳмһҗ мӨ‘ лі‘мқҙ м№ҳмң лҗң нҷҳмһҗмҲҳ
- м¶ңн•ҳлҗң м ңн’Ҳ мӨ‘ л¶Ҳлҹүн’Ҳмқҳ мҲҳ
- лҸ„лЈЁлҘј 20лІҲ мӢңлҸ„н• кІҪмҡ° лҸ„лЈЁм„ұкіө нҡҹмҲҳ
[edit]
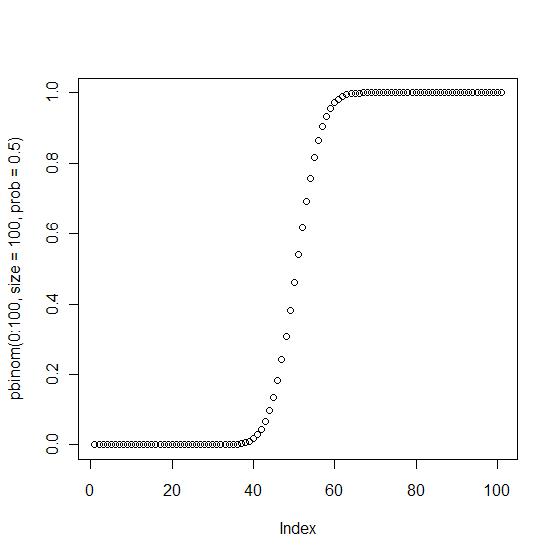
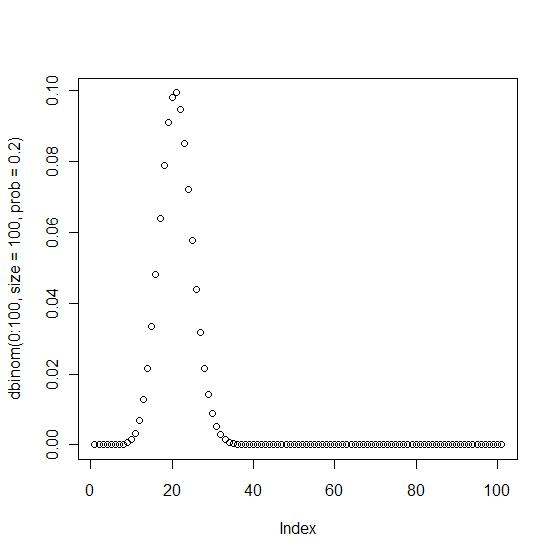
5 нҷ•лҘ л°ҖлҸ„н•ЁмҲҳ #
plot(dbinom(0:100, size=100, prob=0.2))

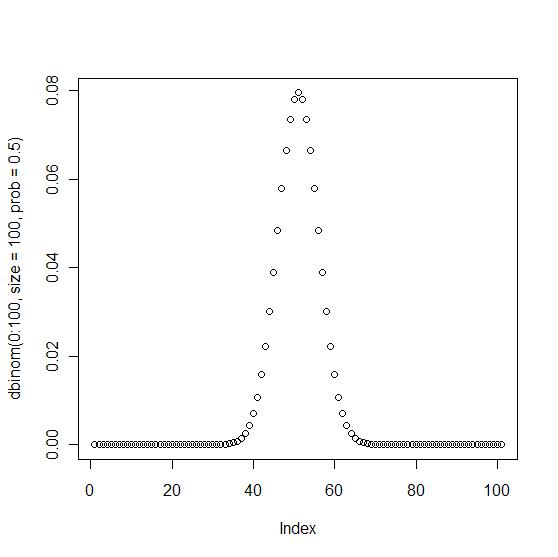
plot(dbinom(0:100, size=100, prob=0.5))

[edit]
9 2н•ӯ분нҸ¬мқҳ м Ғн•©лҸ„ кІҖм • #
> # 100лӘ… мӨ‘ нӣ„ліҙ A м§Җм§Җ:67лӘ…, нӣ„ліҙ Bм§Җм§Җ:33лӘ… мқҙн•ӯкІҖмҰқ Exact binomial test
> binom.test(67, 100, p = 1/2, alternative = "two.sided")
Exact binomial test
data: 67 and 100
number of successes = 67, number of trials = 100, p-value =
0.0008737
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5688272 0.7608015
sample estimates:
probability of success
0.67
>
[edit]
10 нҷ•лҘ кі„мӮ° мҳҲм ң1 #
1. мЈјмӮ¬мң„лҘј л‘җ лІҲ лҚҳм ё лӘЁл‘җ 1мқҙ лӮҳмҳ¬ нҷ•лҘ мқҖ?
> #мЈјмӮ¬мң„ 2нҡҢ лҚҳм§җ. size=2 > #1мқҙ лӮҳмҳ¬ нҷ•лҘ = 1/6 > dbinom(1:2, size=2, prob=1/6) [1] 0.27777778 0.02777778 >мЈјмӮ¬мң„лҘј 1нҡҢ лҚҳм ё 1мқҙ лӮҳмҳ¬ нҷ•лҘ мқҖ 0.27777778мқҙл©°, 2нҡҢ лҚҳм ё лӘЁл‘җ 1мқҙ лӮҳмҳ¬ нҷ•лҘ мқҖ 0.02777778(м•Ҫ 3%)лЎң нҷ•лҘ мқҙ лӮ®мқҖ кІғмқ„ м•Ң мҲҳ мһҲлӢӨ.
2. Aм „м—јлі‘м—җ кұёл Ө нҡҢліөлҗ мҲҳ мһҲлҠ” нҷ•лҘ мқҙ 0.4мқј л•Ң, 15лӘ…мқҙ лі‘м—җ кұёлҰ° кІҪмҡ°
- нҷ•лҘ ліҖмҲҳ Xмқҳ нҸүк· кіј 분мӮ°?
- нҸүк· = 15 * 0.4 = 6 (кё°лҢҖк°’)
- 분мӮ° = 15 * 0.4 * 0.6 = 3.6 (нҸүк· кіј м–јл§ҢнҒј л–Ём–ҙм ё мһҲлҠ”к°Җ? SUM((к°’ - нҸүк· )2) / к°ңмҲҳ
- н‘ңмӨҖнҺём°Ё = SQRT(3.6)
лҢҖ충 6мқҙ к°ҖмһҘ лҶ’мқҖ кјӯм§Җм җмқҙлқјлҠ” кІғмқ„ м•Ң мҲҳ мһҲлӢӨ.
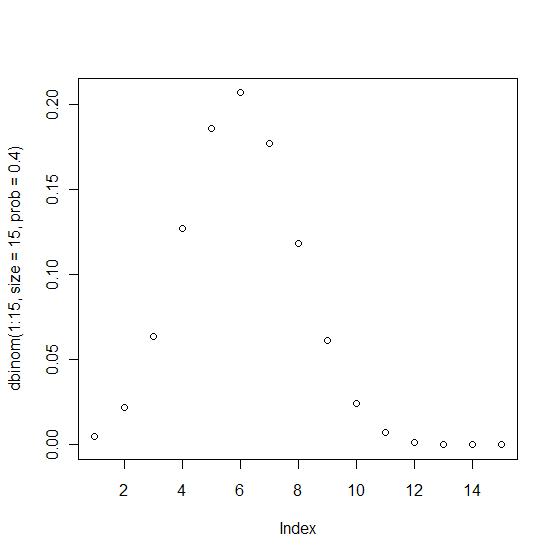
<нҸүк· мқ„ кө¬н•ҳлҠ” лӢӨлҘё л°©лІ•1: лӮңмҲҳнҷңмҡ©>
лӮңмҲҳлҘј нҷңмҡ©н•ҙлҸ„ нҸүк· мқҙ лҢҖ충 6кіј к·јмӮ¬н•ңлӢӨлҠ” кІғмқ„ м•Ң мҲҳ мһҲлӢӨ.
лӮңмҲҳлҘј нҷңмҡ©н•ҙлҸ„ нҸүк· мқҙ лҢҖ충 6кіј к·јмӮ¬н•ңлӢӨлҠ” кІғмқ„ м•Ң мҲҳ мһҲлӢӨ.
> mean(rbinom(1:10000, size=15, prob=0.4)) [1] 6.0037 > mean(rbinom(1:10000, size=15, prob=0.4)) [1] 5.9804 > mean(rbinom(1:10000, size=15, prob=0.4)) [1] 6.0008 > mean(rbinom(1:10000, size=15, prob=0.4)) [1] 6.0188 > mean(rbinom(1:10000, size=15, prob=0.4)) [1] 5.9974 >
- 5лӘ…мқҙ нҡҢліөлҗ нҷ•лҘ
> #15лӘ…мқҙ лі‘м—җ кұёлҰј size=15 > #5лӘ…мқҙ нҡҢліөлҗ нҷ•лҘ > dbinom(1:5, size=15, prob=0.4) [1] 0.00470185 0.02194197 0.06338790 0.12677580 0.18593784 > max(dbinom(1:5, size=15, prob=0.4)) [1] 0.1859378 >
- м Ғм–ҙлҸ„ 10лӘ…мқҙ нҡҢліөлҗ нҷ•лҘ
> 1 - max(pbinom(1:9, size=15, prob=0.4)) [1] 0.0338333 >
- 3лӘ…м—җм„ң 8лӘ…мқҙ нҡҢліөлҗ нҷ•лҘ
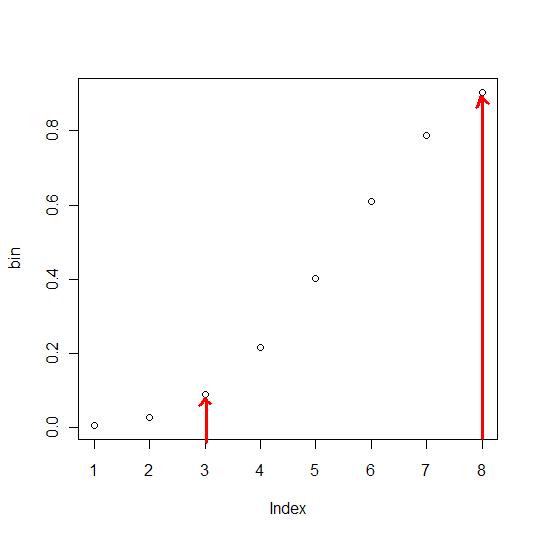
> bin <- pbinom(1:8, size=15, prob=0.4) > 3лӘ…мқҙмғҒмқҙлҜҖлЎң 2к№Ңм§Җ л№јл©ҙ лҗңлӢӨ. > bin[8] - bin[2] [1] 0.8778386 >

3. 4м§Җм„ лӢӨнҳ• 10л¬ём ңлҘј мһ„мқҳлЎң м°Қм–ҙ 3к°ң мқҙн•ҳмқҳ м •лӢөмқ„ л§һм¶ң нҷ•лҘ мқҖ?
> pbinom(1:3, size=10, prob=1/4) [1] 0.2440252 0.5255928 0.7758751 >0.7758751. м•Ҫ 78% нҷ•лҘ мқҙлӢӨ.
4. мЈјмӮ¬мң„ 3к°ңлҘј лҸҷмӢңм—җ лҚҳм§Ҳ л•Ңмқҳ нҷ•лҘ
> dbinom(1:3, size=3, prob=1/6) [1] 0.34722222 0.06944444 0.00462963 >мЈјмӮ¬мң„ 1к°ңл§Ң 1мқҙ лӮҳмҳ¬ нҷ•лҘ мқҖ 0.34722222 мқҙкі , 2к°ңл§Ң 1мқҙ лӮҳмҳ¬ нҷ•лҘ мқҖ 0.06944444 мқҙкі , 3к°ңк°Җ 1мқҙ лӮҳмҳ¬ нҷ•лҘ мқҖ 0.00462963мқҙлӢӨ.
[edit]
11 нҷ•лҘ кі„мӮ° мҳҲм ң2 #
5. мҙқ 10л¬ём ң, 5м§Җм„ лӢӨнҳ•(5к°ңмқҳ лӢө к°ҖмҡҙлҚ° 1к°ңл§Ң м •лӢө) м°Қмқ„ л•Ң 9к°ңлҘј л§һм¶ң нҷ•лҘ мқҖ?
> dbinom(1:9, size=10, prob=1/5)[9] [1] 4.096e-06
6. лҸҷм „мқ„ лҚҳм ём„ң м•һл©ҙмқҙ лӮҳмҳӨл©ҙ мҳӨлҘёмӘҪмңјлЎң 1лӢЁмң„ мқҙлҸҷн•ҳкі , л’·л©ҙмқҙ лӮҳмҳӨл©ҙ мҷјмӘҪмңјлЎң 1лӢЁмң„ мқҙлҸҷн• л•Ң
- мІҳмқҢм—җ мӣҗм җм—җм„ң мҳӨлҘёмӘҪ 2лӢЁмң„ кұ°лҰ¬м—җ мһҲлӢӨ н• л•Ң, мӣҗм җмңјлЎң лҸҢм•„мҳ¬ нҷ•лҘ
> pbinom(1:10, size=10, prob=1/2) [1] 0.01074219 0.05468750 0.17187500 0.37695313 0.62304687 0.82812500 [7] 0.94531250 0.98925781 0.99902344 1.00000000 > bin <- pbinom(1:10, size=10, prob=1/2) > #мҳӨлҘёмӘҪмңјлЎң 4лӢЁмң„, мҷјмӘҪмңјлЎң 6лӢЁмң„ мӣҖм§Ғмқҙл©ҙ мӣҗм җ > bin[6] - bin[5] [1] 0.2050781 > #лҳҗлҠ” > bin <- dbinom(1:10, size=10, prob=1/2) > bin [1] 0.0097656250 0.0439453125 0.1171875000 0.2050781250 0.2460937500 [6] 0.2050781250 0.1171875000 0.0439453125 0.0097656250 0.0009765625 > #мҷјмӘҪ 4лӢЁмң„ мқҙлҸҷ нҷ•лҘ лҳҗлҠ” мҳӨлҘёмӘҪ 6лӢЁмң„ мқҙлҸҷн• нҷ•лҘ л§Ң кө¬н•ҳл©ҙ лҗңлӢӨ. > bin[4] [1] 0.2050781 > bin[6] [1] 0.2050781
- мІҳмқҢм—җ мӣҗм җм—җ мһҲмқ„ л•Ң, мқҙ мӢңн–үмңјлЎң мӣҗм җм—җм„ң 2лӢЁмң„ мқҙлӮҙм—җ мһҲмқ„ нҷ•лҘ
> #мӣҗм җм—җм„ң 2лӢЁмң„ мқҙлӮҙм—җ мһҲлҠ” кІҪмҡ° > #мҷјмӘҪ:5, мҳӨлҘёмӘҪ:5 > #мҷјмӘҪ:4, мҳӨлҘёмӘҪ:6 > #мҷјмӘҪ:6, мҳӨлҘёмӘҪ:4 > bin <- dbinom(1:10, size=10, prob=1/2) > sum(bin[4:6]) [1] 0.65625
8. нҷ”нҲ¬лҠ” мҙқ 48мһҘмқҙлӢӨ. 12мў…мқҙл©°, к°Ғ 4мһҘм”© м§қмқ„ мқҙлЈ¬лӢӨ. 1л§Өм”© 4лІҲ лҪ‘мқ„ л•Ңм—җ мҶЎн•ҷ(мқј)мқ„ 3мһҘ лҪ‘мқ„ нҷ•лҘ
> dbinom(1:3, size=4, prob=4/48)[3] [1] 0.002121914мЎ°лӮё лӮ®мқҖ нҷ•лҘ мқҙлӢӨ. мқҙлҹ° лҸ„л°•мқҖ м ҲлҢҖ н•ҳм§Җ л§җм•„м•јкІ кө¬лЁј..
п»ҝ