DataBaser.Net: 분산분석

1 개요
2 무작정 해보기
3 일원 분산분석
4 반복이 없는 다원 분산 분석
5 반복이 있는 다원 분산분석
6 비모수적 방법
7 정리중..

1 개요 #

평균의 차이 검정
전제조건
- 독립성: 각 집단은 서로 독립적이어야 한다.
- 정규성: 각 집단은 정규분포를 이루어야 한다.
- 불편성: 각 집단별 분산의 정도가 비슷해야 한다.
독립변수(or 인자 or factor)와 종속변수의 관계를 분석하는 기법. 예를 들어, 사무직, 생산직, 서비스직의 임금 차이를 분석할 경우 사무직, 생산직, 서비스직은 독립변수(요인)이고, 임금은 종속변수다. 그리고 사무직, 생산직, 서비스직는 인자수준(factor levle)이라고 한다.
일원 분산분석(one-way ANOVA): 단 하나의 인자를 분석 대상으로 할 경우
이원 분산분석(two-way ANOVA): 두 개의 인자를 분석 대상으로 할 경우
다원 분산분석(multi-way ANOVA): 세 개 이상의 인자를 분석 대상으로 할 경우
요인효과 = 주효과 + 교호작용
제곱평균(=불편분산) = 편차제곱의 합 / 자유도

2 무작정 해보기 #

use tempdb;

--drop table 성적
create table 성적
(
	통계 int
,	결석 int
,	수학 int
);

insert 성적 values (85, 3, 65);
insert 성적 values (74, 7, 50);
insert 성적 values (76, 5, 55);
insert 성적 values (90, 1, 65);
insert 성적 values (85, 3, 55);
insert 성적 values (87, 3, 70);
insert 성적 values (94, 1, 65);
insert 성적 values (98, 2, 70);
insert 성적 values (81, 4, 55);
insert 성적 values (91, 2, 70);
insert 성적 values (76, 3, 50);
insert 성적 values (74, 4, 55);

> library("RODBC")
> conn <- odbcConnect("26")
> data <- sqlQuery(conn, "SELECT 통계, 수학, 결석 FROM tempdb.dbo.성적")
> a <- aov(통계 ~ 수학 + 결석, data)
> a
Call:
   aov(formula = 통계 ~ 수학 + 결석, data = data)

Terms:
                    수학     결석 Residuals
Sum of Squares  541.6927  61.9657  124.5916
Deg. of Freedom        1        1         9

Residual standard error: 3.720687 
Estimated effects may be unbalanced
> summary(a)
            Df Sum Sq Mean Sq F value    Pr(>F)    
수학         1 541.69  541.69 39.1297 0.0001487 ***
결석         1  61.97   61.97  4.4762 0.0634803 .  
Residuals    9 124.59   13.84                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
>

결과해석

가설
- 귀무가설: 요인별 차이가 없다.
- 대립가설: 요인별 차이가 있다.
수학의 p-value = 0.0001487로 유의수준 0.05보다 작으므로 대립가설을 뻑낼 이유를 찾지 못했다. 그러므로 수학점수와 통계점수와는 차이가 있다.
결석의 p-value = 0.0634803로 유의수준 0.05보다 크므로 대립가설은 뻑낼 이유를 찾았다. 그러므로 귀무가설을 지지한다. 그러므로 통계점수는 결석수에 따라서 좌지우지 된다고 할 수 있다.

[edit]

3 일원 분산분석 #

c1 <- c(3.6, 4.1, 4.0)
c2 <- c(3.1, 3.2, 3.9)
c3 <- c(3.2, 3.5, 3.5)
c4 <- c(3.5, 3.8, 3.9)
data <- data.frame(c1,c2,c3,c4)

#데이터를 만들어야 한다. stack()
data <- stack(data)
summary(aov(values ~ ind, data))

결과는 다음과 같다.

            Df  Sum Sq Mean Sq F value Pr(>F)
ind          3 0.56250 0.18750    2.25 0.1598
Residuals    8 0.66667 0.08333

결과의 해석

가설
- 귀무가설: 차이가 없다.
- 대립가설: 차이가 있다.
p-value = 0.1598 으로 대립가설이 뻑날 1종 오류의 확률이 0.05보다 크다. 그러므로 귀무가설을 지지한다.
즉, 3개 그룹의 평균 차이는 없다.

[edit]

4 반복이 없는 다원 분산 분석 #

실험실 <- c(rep("1",4), rep("2",4), rep("3",4))
식품 <- c(rep(c("A","B","C","D"),3))
관측치 <- c(3.6,3.1,3.2,3.5,4.1,3.2,3.5,3.8,4.0,3.9,3.5,3.8)
data <- data.frame(관측치, 실험실, 식품)
data
summary(aov(관측치 ~ 식품 + 실험실), data)

결과는 다음과 같다.

> data
   관측치 실험실 식품
1     3.6      1    A
2     3.1      1    B
3     3.2      1    C
4     3.5      1    D
5     4.1      2    A
6     3.2      2    B
7     3.5      2    C
8     3.8      2    D
9     4.0      3    A
10    3.9      3    B
11    3.5      3    C
12    3.8      3    D
> summary(aov(관측치 ~ 식품 + 실험실), data)
            Df  Sum Sq Mean Sq   F value    Pr(>F)    
(Intercept)  1 155.520 155.520 4241.4545 8.813e-10 ***
식품         3   0.540   0.180    4.9091   0.04692 *  
실험실       2   0.420   0.210    5.7273   0.04062 *  
Residuals    6   0.220   0.037                        
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Warning messages:
1: In model.matrix.default(mt, mf, contrasts) :
  variable '식품' converted to a factor
2: In model.matrix.default(mt, mf, contrasts) :
  variable '실험실' converted to a factor
3: In Ops.factor(left) : ! 인자에 대해서 무의미합니다
4: In Ops.factor(left) : ! 인자에 대해서 무의미합니다
>

결과 해석

가설
- 귀무가설: 요인별 차이가 없다.
- 대립가설: 요인별 차이가 있다.
식품의 p-value = 0.04692이므로 0.05보다 작다. 즉, 대립가설을 뻑낼 건덕지를 찾지 못했다. 귀무가설 기각. 그러므로 식품별로 관측값의 평균이 차이가 있다.
실험실의 p-value= 0.04062이므로 0.05보다 작다. 즉, 대립가설을 뻑낼 건덕지를 찾지 못했다. 귀무가설 기각. 그러므로 실험실별로 관측값의 평균이 차이가 있다.

[edit]

5 반복이 있는 다원 분산분석 #

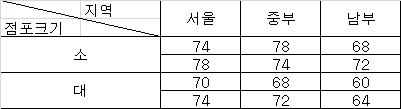
"반복이 있는"이란 뜻은 다음과 같은 뜻이다. 즉, 중복된 데이터가 있음을 뜻한다. ("select distinct 점포크기, 지역"과 "select 점포크기, 지역"은 다르다.)

지역 <-c(rep("서울",4), rep("중부",4), rep("남부",4))
점포크기 <- rep(c("소","소","대","대"), 3)
관측치 <- c(74,78,70,74,78,74,68,72,68,72,60,64)
data <- data.frame(관측치, 지역, 점포크기)

> data
   관측치 지역 점포크기
1      74 서울       소
2      78 서울       소
3      70 서울       대
4      74 서울       대
5      78 중부       소
6      74 중부       소
7      68 중부       대
8      72 중부       대
9      68 남부       소
10     72 남부       소
11     60 남부       대
12     64 남부       대

반복이 있는 다원 분산분석을 실시 할 경우, 가장 먼저 교호작용이 있는지 살펴보아야 한다. 교호작용은 교호작용도(interaction plot)을 이용하면 된다. R의 경우 다음과 같이 하면 된다.

par(mfrow=c(1,2))
interaction.plot(지역,점포크기,관측치)
interaction.plot(점포크기,지역,관측치)

결과는 다음과 같다. 만약 교호작용이 발생한다면 그래프가 교차하는 부분이 생긴다.

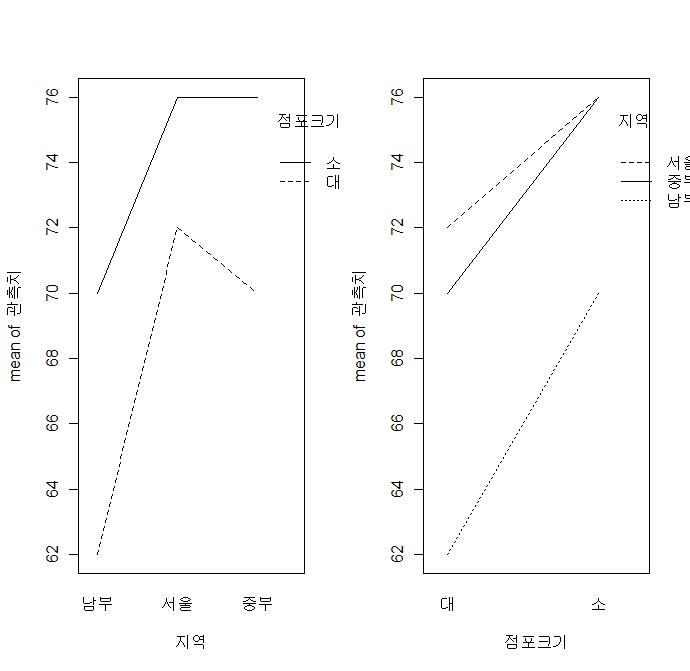
교호작용이 없는 것을 알았지만 그냥 한 번 교호작용을 하지는도 살펴보도록 하자.

summary(aov(관측치 ~ 점포크기 + 지역 + 점포크기:지역, data))

결과는 아래와 같다.

              Df Sum Sq Mean Sq F value    Pr(>F)    
(Intercept)    1  60492   60492  7561.5 1.558e-10 ***
점포크기       1    108     108    13.5   0.01040 *  
지역           2    152      76     9.5   0.01382 *  
점포크기:지역  2      8       4     0.5   0.62974    
Residuals      6     48       8                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Warning messages:
1: In model.matrix.default(mt, mf, contrasts) :
  variable '점포크기' converted to a factor
2: In model.matrix.default(mt, mf, contrasts) :
  variable '지역' converted to a factor
3: In Ops.factor(left) : ! 인자에 대해서 무의미합니다
4: In Ops.factor(left) : ! 인자에 대해서 무의미합니다

결과해석

가설
- 귀무가설: 요인별 차이가 없다.
- 대립가설: 요인별 차이가 있다.
점포크기 p-value = 0.01040 로 유의수준 0.05보다 작으므로 대립가설을 뻑낼 이유를 찾지 못했다. 대립가설을 지지하고, 귀무가설을 기각한다. 즉, 점포크기에 따라서 관측치(가격)의 차이가 있다.
지역 p-value = 0.01382 로 유의수준 0.05보다 작으므로 대립가설을 뻑낼 이유를 찾지 못했다. 대립가설을 지지하고, 귀무가설을 기각한다. 즉, 지역에 따라서 관측치(가격)의 차이가 있다.
점포크기:지역 p-value = 0.629742 로 유의수준 0.05보다 크므로 대립가설을 뻑낼 이유를 찾았다. 귀무가설을 지지한다. 즉, 점포크기와 지역의 복합효과에 대한 관측치(가격)의 차이는 없다. (교호작용 없음)

[edit]

6 비모수적 방법 #

크루스칼-왈리스 순위합 검증(kruskcal-wallis rank sum test)
비모수: 소표본, 정규성 가정을 전제하기 어려울 경우
kruskcal.test() 이용

> #세 그룹의 기관지 점막섬모의 효율성을 측정한 결과
> x <- c(2.9, 3.0, 2.5, 2.6, 3.2) #정상인
> y <- c(3.8, 2.7, 4.0, 2.4)      #폐쇄성 기도질환자
> z <- c(2.8, 3.4, 3.7, 2.2, 2.0) #석면폐증 환자
> data <- data.frame(x,y,z)
이하에 에러data.frame(x, y, z) : 인수는 다른 열수를 의미합니다 5, 4
> kruskal.test(data)

        Kruskal-Wallis rank sum test

data:  data 
Kruskal-Wallis chi-squared = 0.7714, df = 2, p-value = 0.68

>

결과해석

가설
- 귀무가설: 차이가 없다.
- 대립가설: 차이가 있다.
p-value = 0.68이므로 유의수준 0.05에서 대립가설은 뻑. 그러므로 귀무가설 지지
즉, 3그룹의 분진제거에 대한 점막섬모 효율성은 차이가 없다.

다음과 같이 그룹을 만들어서 할 수도 있다. (g가 그룹이다)

s <- c(x,y,z)
g <- rep(1:3, c(length(x),length(y),length(z)))
data <- data.frame(s,g)
kruskal.test(s,g)

> s <- c(x,y,z)
> g <- rep(1:3, c(length(x),length(y),length(z)))
> data <- data.frame(s,g)
> kruskal.test(s,g)

        Kruskal-Wallis rank sum test

data:  s and g 
Kruskal-Wallis chi-squared = 0.7714, df = 2, p-value = 0.68

>

[edit]

7 정리중.. #

{현대실험계획법, 박성현, 민영사}의 예제 3.1

#3-1
x <- read.table(header=T, text="
factorLevel  characteristicValue
A1	8.44
A1	8.36
A1	8.28
A2	8.59
A2	8.91
A2	8.6
A3	9.34
A3	9.41
A3	9.69
A4	8.92
A4	8.92
A4	8.74") 
head(x)

aov.out <- aov(characteristicValue~factorLevel, data=x)
summary(aov.out)
drop1(aov.out,~.,test="F")

model.tables(aov.out, type="means", se=T)
model.tables(aov.out, type="effects", se=T)

TukeyHSD(aov.out)
plot(TukeyHSD(aov.out))


library(gplots)
plotmeans(characteristicValue~factorLevel, data=x)


lm.out <- lm(characteristicValue~factorLevel, data=x)
summary(lm.out)
summary.aov(lm.out)


#등분산 검정
bartlett.test(characteristicValue~factorLevel, data=x)
fligner.test(characteristicValue~factorLevel, data=x)
#library(HH)
#hov(characteristicValue~factorLevel, data=x)
#library(lawstat)
#levene.test(characteristicValue~factorLevel, data=x)

Retrieved from http://www.databaser.net/moniwiki/wiki.php/분산분석
last modified 2018-04-13 23:12:53

Contents

1 개요 #

2 무작정 해보기 #

3 일원 분산분석 #

4 반복이 없는 다원 분산 분석 #

5 반복이 있는 다원 분산분석 #

6 비모수적 방법 #

7 정리중.. #