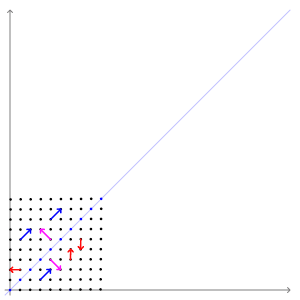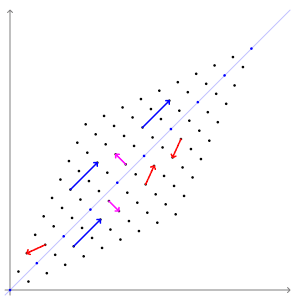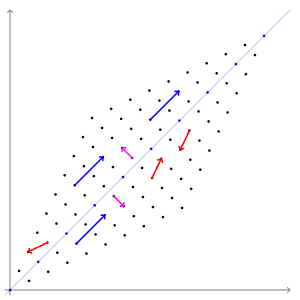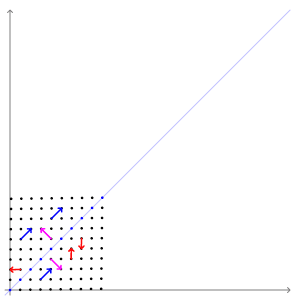
아래 그림을 보자. (움직이는 그림이다)
 --출처: https://upload.wikimedia.org/wikipedia/commons/0/06/Eigenvectors.gif
--출처: https://upload.wikimedia.org/wikipedia/commons/0/06/Eigenvectors.gif
파란색, 보라색(?) 벡터는 크기가 변해도 방향은 변하지 않았다. 빨간색 벡터는 크기가 변하면 방향도 변한다.
크기가 변했을 때 방향도 변하면 고유벡터가 아니다.
그림을 잘보면 파란색과 보라색 벡터(고유벡터)는 직교(orthogonal)하다.
파란색과 보라색 벡터만 보면 주성분 분석에서 고유값과 고유벡터를 왜 사용하는지 알 수 있다.
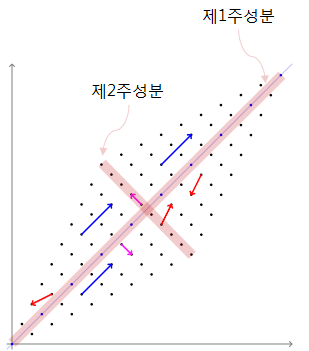
위 그림이 산점도라면, 주성분 분석의 결과를 시각화하면 아래와 같을 것이다.